Stress distribution on maxillary central incisor under similar traumatic situations with different loading forces: a 3-D finite element analysis

 

Distribuição de estresse em incisivo central superior sob situações traumáticas semelhantes com diferentes cargas: uma análise tridimensional de elementos finitos

 

 

Bruno Rocha da Silva ^I; Nayane Cavalcante Ferreira ^II; José Jeová Siebra Moreira-Neto ^III; Francisco Ilson da Silva Jr ^IV; Edson Holanda Teixeira ^I; Andréa Silvia Walter de Aguiar ^III

^I LIBS, Laboratório Integrado de Biomoléculas, Universidade Federal do Ceará, Fortaleza, CE, Brasil
^II Universidade Federal do Ceará, Fortaleza, CE, Brasil
^III Departamento de Dentística, Universidade Federal do Ceará, Fortaleza, CE, Brasil
^IV Departamento de Engenharia Mecânica, Universidade Federal do Ceará, Fortaleza, CE, Brasil

Contact: brunorocha747@gmail.com, nayanecferreira@gmail.com, jeova@ufc.br, ilson@ufc.br, edson@ufc.br, andrea.aguiar@ufc.br

 

 

---

 

ABSTRACT

Aim: The present study aimed to analyze the stress distribution in the dentoalveolar structures of a maxillary central incisor submitted to two situations of impact loading. Materials and Methods: The following loading forces were applied using a three-dimensional finite element model: a force of 500 N at an angle of 45° on the buccal surface of the crown and a 2000 N force acting in the same direction and surface of the tooth. Results: Harmful stress was observed in the second situation, suggesting damage to both the tooth and adjacent tissue. However, the damage found in soft tissues such as dental pulp, was negligible. Conclusion: Injuries resulting from the traumatic situations were more damaging to the integrity of the tooth and its associated hard-tissue structures.

Uniterms: Tooth injuries. Finite element analysis. Biomechanics. Computing methodologies. Threedimensional imaging.

---

 

RESUMO

Objetivo: O objetivo deste estudo foi analisar a distribuição de tensões nas estruturas dentoalveolares de um incisivo central superior submetido a duas situações de carga de impacto. Materiais e métodos: As forças de carga que se seguem foram aplicadas usando um modelo tridimensional de elementos finitos: uma força de 500 N a um ângulo de 45° sobre a superfície vestibular coronária; uma força de 2000 N atuando no mesmo sentido e no mesmo ponto sobre a superfície do dente. Resultados: Tensões prejudiciais foram observadas na segunda situação, o que sugere danos ao dente e ao tecido adjacente. No entanto, o dano encontrado em tecidos moles, tais como polpa dentária foi insignificante. Conclusão: Lesões decorrentes de situações traumáticas foram mais prejudiciais para a integridade do dente e os seus estruturas associadas ao tecido duro.

Descritores: Traumatismos dentários. Análise de elementos finitos. Biomecânica. Metodologias computacionais. Imagem tridimensional.

---

 

 

INTRODUCTION

Dental trauma is one of the main emergencies in dentistry. However, the precise biomechanical characteristics of dental trauma and their repercussions on adjacent tissues are largely unknown with little experimental evidence.^1-3

Dentoalveolar joint (DAJ) injuries are caused by the sum of the effects of impact applied to the tooth. These effects can be direct when the consequences of trauma occur in the area of impact, such as tooth fractures, or indirect when the stress produced by the impact propagates to adjacent tissues and causes damage to these regions, such as root resorption resulting from periodontal ligament (PDL) necrosis.^4,5

Several methods have been developed in an attempt to better understand the stress distribution inside the dentoalveolar joint (DAJ). Such methodologies include photoelastic models, analytical mathematical models, and mathematical analyses, such as the finite element method (FEM).^6-8

In FEM, the behavior of a particular physical system is mathematically simulated. A continuous structure is divided into different elements, which maintain the properties of the original structure. Each of these elements is described by differential equations and solved using mathematical models selected according to the data under investigation.^9,10

FEM allows the researcher to create models for complex structures, reproducing the irregular geometries of either natural or artificial tissues, e.g. the dentoalveolar articulation. In addition, FEM allows one to modify the parameters of those geometries, which makes it possible to apply a force or a system of forces to any point and/or in any direction, thereby providing information on movement and on the degree of tension and compression forces caused by these loads.^8,11

The aim of this study was to analyze the stress distribution in the dentoalveolar structures of a maxillary central incisor submitted to two similar situations of traumatic impact with different loading forces.

 

MATERIALS AND METHODS

Three-dimensional geometrical model design

The methodology used to obtain three-dimensional finite element model was similar to that applied previously by the authors.¹² This methodology allowed obtaining relevant results in addition to comprehend a good part of the current scientific literature. For modeling of the DAJ, computed tomography (CT) of the middle third of the surface comprising the entire region of the jaw was performed in a 23-year-old healthy male volunteer without a history of dental anomalies, dental caries, periodontal diseases or dental trauma in the region of the maxillary incisors. The patient received information about the objectives of the study and signed a free informed consent form.

CT was performed with a GE HiSpeed NX/i tomograph (General Electric, Denver, CO) using the following acquisition parameters: 120 kV, 150 mA, a 512 x 512 matrix, a field of view of 14 x 14 cm, and a slice thickness of 0.5 mm, resulting in a voxel size of 0.273 mm. The number of reconstruction planes was 511 in the anteroposterior direction, 511 in the lateral-lateral direction, and 71 in the cleidocranial direction. The images were saved in Digital Imaging Communications in Medicine) (DICOM) format.

After selection of the sections corresponding to the right maxillary central incisor, the images were exported to the ScanIP software, version 3.1 (Simpleware Corporation, UK) for image discretization to obtain the three-dimensional geometric model used for the FE model in the next phase. Image discretization was performed based on the Hounsfield units referring to each component of the DAJ.

Finite element mesh generation

Next, the geometric model was exported to the ScanFE software, version 3.1 (Simpleware Corporation), which generated the FE mesh (Figure 1). This mesh consisted of 241.944 elements, including 14.391 hexagonal elements and 227.553 tetrahedral elements. The PDL was simulated using a resource called contact surface because of the impossibility of direct modeling of the tomographic scan. For this purpose, the ScanFE software created a thin layer of interposed elements between the two distinct layers of the model. This layer was included between the dentin and lamina dura with a thickness average of 0.2 mm, simulating the PDL^11,13,14. However, the PDL is not uniformly thick. In this manner, the thickness and shape of the PDL were adjusted according to the conformation of the alveolus. This step is crucial regarding the PDL's decisive influence of load transfer and stress/strain distribution in the tooth, the PDL itself and the surrounding bone.^5,15 The cementum layer was not modeled because of its small thickness and physical properties that are similar to those of dentin.¹⁶

 

 

 

 

 

Defining the simulation and loading conditions

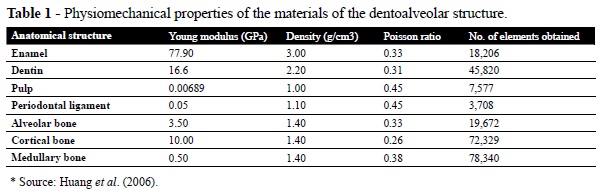
Once the mesh had been completed, it was exported to the Ansys software, version 11.0 (Swanson Analysis Systems, Houston, PA) and the specific properties [Young modulus (E), Poisson ratio (v) and density (d)] of each material of the model were added (Table 1).^5,15,16

The conditions of analysis to simulate this model were considered when it behaved in a homogeneous and isotropic manner, i.e., all material properties were identical in all directions, and with a linear elastic behavior, in which deformation of the structure occurs linearly. After establishment of the analysis conditions, two situations of traumatic impact were simulated: a) a loading force of 500 N applied at a 45° angle, acting on the buccal surface of the crown in its central region (F1) and b) a loading force of 2000 N, acting in the same angle, surface, and region of the tooth (F2) (Figure 2). The loading force was applied gradually, starting at 0 N until the

 

 

 

 

 

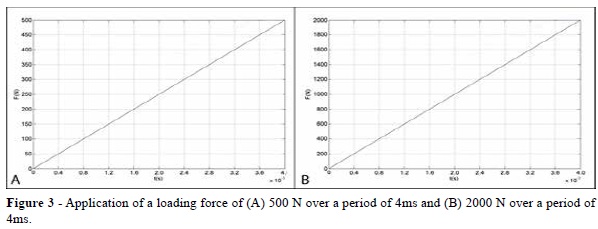
maximum of 500 N for the first situation and 2000 N for the second had been reached over a period of 4 milliseconds (ms) (Figures 3A and 3B). This characterizes a transient dynamic analysis in which a load is applied gradually until a peak is reached within a given period of time. This type of analysis was chosen, as it provides a more realistic simulation of the mechanism of dental trauma.^5,13-16

The model verification was provided by the use of complementary numerical methods beyond the use of a commercial finite element software, ensuring the validation of the method itself, as well a correct application of boundary conditions, material properties, and load/force applications.^11,13,14

All steps of this study from image processing to the analysis and visualization of the results were performed using a Celeron 723 computer (Intel, Santa Clara, CA), equipped with a 250-Gb Hard Drive (HD) and 2.0-Gb RAM memory, at the Information Technology Laboratory of the Department of Mechanical Engineering, Federal University of Ceará (UFC), between December 2009 and May 2010. The study was approved by the UFC Research Ethics Committee (protocol number 38/10).

 

RESULTS

First analysis results

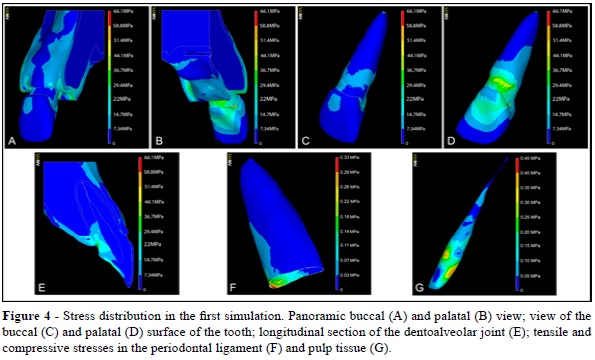
The obtained results were quantified using the Von Mises stress index. This index provides a final result of stress areas, i.e., areas where the material suffers from some type of tension or compression, and was chosen because of its capacity to better demonstrate stress distribution in tissues. The results are presented as color scaled images in which each color corresponds to a stress-value interval in MPa.

Figures 4A and 4B show the stress distribution on the buccal and palatal surface during the first simulation. In the crown region, stress levels were close to zero throughout most of the buccal surface, whereas on the palatal surface stress levels ranged from 0 to 29.4 MPa and were concentrated in the region of the cingulum. Figures 4C and 4D illustrate the stress distribution along the dental tissue on the buccal and palatal surfaces, as well as high stress areas. The highest stress concentration was observed in the cervical dentin due to its compression against the adjacent alveolar bone. In this area, stress levels reached a peak of 51.4 MPa and were found around the entire palatal region and extending to the inner portion of the tooth.

A longitudinal section of the structure revealed the propagation of stress to the inner portion of the DAJ (Figure 4E). In this view, stress distribution on the dental enamel was noted, but showed no continuity to dentinal tissue, dissipating through the enamel to cervical areas. In these cervical regions, stress distribution was observed along the inner portion of the root, extending to the cervical and middle third of the root, with values ranging from 7.34 to 36.7 MPa.

Stress also developed in the dental pulp and PDL, but the stress values were low (< 1 MPa). In the dental pulp, the highest stress levels were observed in the crown region, with the stress peak found on the palatal surface. By contrast, in the PDL, stress levels were concentrated in the cervical area with values ranging from 0 to 0.33 MPa (Figures 4F and 4G).

 

 

 

Second analysis results

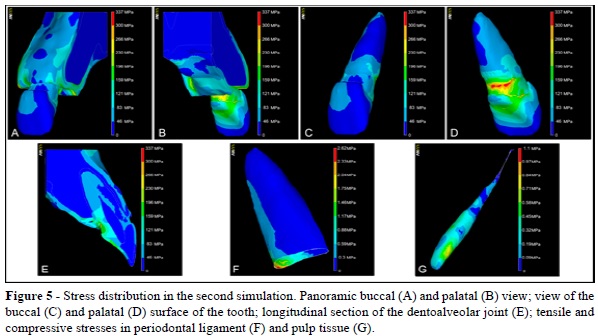
A similar stress concentration and distribution was observed in the second impact situation, when compared to the previous simulation, due to the same position and direction of the loading force. However, the stress values proved to be higher, ranging from 0 to 196 MPa on the buccal side of the crown, neck, and bone, with a stress zone peak found on the palatal surface of these structures (Figures 5A and 5B).

The highest stress concentration was observed in the cervical dentin due to its compression against the adjacent alveolar bone. In this area, stress levels reached a peak of 337 MPa and were found around the entire palatal region and extending to the inner portion of the tooth. In this simulation, stress was almost exclusively concentrated on the palatal surface, mainly enamel, dentin, and cortical bone. In contrast to the previous simulation, internal stress dissipated to the middle and apical third of the root, with values ranging from 0 to 159 MPa (Figures 5C and 5D).

A longitudinal section of the dentoalveolar structure showed a stress distribution along the tooth towards the apical region, with stress values ranging from 46 to 159 MPa in its largest area with small zones of critical stress values. The discontinuity in the stress distribution from the enamel layer to the dentin layer was similar to that observed in the previous simulation (Figure 5E).

Stress was low in the dental pulp but was still higher than those obtained in the previous simulation, with a peak of 1.1 MPa (Figure 5G). However, the PDL stress values and distribution proved to be significantly different from the first simulation, given that the stress area reached the apical third and, in the cervical third, the stress values ranged from 0.88 to 2.62 MPa (Figure 5F).

 

 

 

DISCUSSION

FE analysis allows the researcher to mathematically simulate the behavior of a physical system by computer.^6,8 These rapid technological advances have rendered FE modeling an important tool in dentistry, with a significant increase in the number of publications on FE analysis, especially its versatility and efficacy in the analysis of dental trauma.⁷

The maxillary central incisor is the tooth most frequently affected by dental trauma and was therefore chosen for FE modeling.^1-3,17 However, the direction, position, and magnitude of the traumatic force are key factors for the determination of its consequences on the tooth.^18,19 Although the frontal traumas are the most common, the knowledge about the impact distribution during oblique dental trauma is extremely important to fully understand the biomechanics of dentoalveolar trauma to periodontal structures.

The chosen forces to simulate the traumatic injury were 500 N and 2000 N. This choice was due to the dearth of studies comparing the biomechanical behavior of DAJ when submitted to the same sort of trauma but with different impact forces, a fact that can directly influence the patient's clinical repercussions. Some studies use a force of 800 N to simulate mild traumatic situations, which results, in most cases, in only enamel surface fractures.^5,13-16 However, a study by Miura and Maeda showed that a force of 100 N, when applied horizontally on the buccal surface of the tooth, could already generate an avulsion.¹⁶

The methodology of this study was based on other authors who used the finite element method with the same purpose of simulating the dentoalveolar structure. Concerning the validation of the finite element mesh, a simple complementary numerical method was used in an attempt to achieve a greater reliability of results and a confirmation of the cohesion of dental structures, along with the use of a commercial software already grounded in scientific literature.^{5,10,12,13,15,16}

Due to the application of the same impact direction, differences in stress distribution in the crown region of the tooth were not observed between the simulations. Some other factors were also similar, such as the lack of stress dissipation to the crown dentin, a fact that can be explained by the physicomechanical properties of dental enamel. Although enamel is not very resistant to trauma, it does show a high capacity of stress absorption and dissipation.²⁰ Therefore, the complex microstructure of enamel, consisting of crystalline prisms, forms a protective physiological layer covering the teeth.^21,22

According to Huang et al., enamel fracture lines already appear at a stress value of 50 MPa.¹⁵ The stress distribution and values obtained in second simulation suggest the possibility of enamel fracture lines in areas of higher stress concentration since the maximum value found (46 to 83 MPa) is much higher than those reported in their study.¹⁵

Despite the high stress values found in the second simulation, the occurrence of root fracture is unlikely since the stress zones among the root were not continuous. Nevertheless, according to Stuart et al., in 2006, the force necessary to cause root fracture must be in the order of 1,600 N.¹⁷ In addition, clinical factors, such as the mechanical properties of dentin, are unfavorable to root fractures, since dentin possesses a higher deformation capacity until fracture than does enamel.²³ This finding agrees with epidemiological data showing a low prevalence of root fracture among dental trauma.24 Similar stress distribution can be found in studies on bruxism, in which a buildup of stress concentration could be identified in the cervical regions; however, this type of situation will only be able to generate clinical consequences when applied over a long period of time, resulting in non-carious cervical lesions.^9,25

In both simulations, the tensile zone was found on the buccal surface and the compressive zone on the palatal surface. This simulation was characterized by a larger area of stress convergence originating from compression against the palatal alveolar bone crest and the accumulation of stress dissipated by the enamel. Dentin fracture in the palatal cervical region is unlikely because of the capacity of dentin to withstand high compressive loads and because of its physicomechanical properties.²³ In addition, a wide distribution of stress to the apical portion of the root was evident in the second simulation. This finding may be associated with the applied loading force, given that, in the first situation, a lower load of 500 N was applied. This finding demonstrates that despite similar traumatic situations, the loading force of impact plays a key role in the biomechanical distribution of dentoalveolar trauma.

Regarding the PDL, the large area of compression generated in the cervical region in the second situation suggests a higher risk of damage to periodontal structures, either due to the squeezing of PDL fibers or to the fracture of the adjacent alveolar bone. This fact is also substantiated by findings from Natali (2003), reporting that the PDL withstands stress levels of 2.4 MPa, a value reached in the second simulation.26

Concerning the modeling process used to simulate the PDL, studies evaluating stress on the PDL emphasize the importance of using viscoelastic models due to its proximity to the real situation, allowing for the analysis of PDL under time-dependent forces.^5,15,27,28 However, some authors demonstrate that such models are best used in cases in which the traumatic force is applied for longer periods of time, situations found in studies on orthodontic tooth movement.²⁹ According to the same author, studies using viscoelastic models are more complex and, in some cases, do not promote a significant difference of results.²⁹ Thus, according to Poiate et al., studies in which the PDL will be subjected to injury for a short period of time, as occurs in dentoalveolar trauma, linear elastic models are able to simulate the behavior of the PDL satisfactorily.^11,13

In view of the lack of data in the literature, the comparative values of maximum stress load supported by dental pulp do not allow one to confirm the significant pulp damage, although clinical studies suggest that mild trauma (e.g., concussion/ subluxation) may cause pulp necrosis.³⁰ Tanaka et al. reported that dental pulp can withstand tensile/ compressive forces of 2.94 MPa, a value higher than the values found in both simulations, which was 0.45 MPa for the first simulation and 1.1 MPa for the second, thus suggesting that the applied forces were unable to cause pulp damage.³⁰

Despite being an extremely viable method for simulations in biological systems, the FEM has some limitations, which sometimes render it impossible to extrapolate results obtained in clinical practice. Limitations exists, such as the lack of data on biological structures (as gingival tissue and vascular structures), in addition to the absence of a viable and accurate model of the behavior of dentoalveolar complex^9,10

However, the results obtained in this study are able to shed light on some aspects that are still poorly covered in dental traumatology literature. These findings may help to clarify clinical situations that present unexpected outcomes but that may be justified by the biomechanical distribution of the trauma itself.^4,6

 

CONCLUSION

In the present study, only the second simulation resulted in a significant biomechanical damage to the dentoalveolar structure, with the observation of high stress areas in the cervical regions of the root, though stress areas were also detected in the crown enamel and buccal alveolar bone. Although the force applied was not sufficient to cause major damage to the DAJ, the present study suggests that even under similar circumstances, the mode of distribution of loading forces applied to the DAJ may vary depending on the load itself.

 

REFERENCES

1. Bastone EB, Freer TJ, McNamara JR. Epidemiology of dental trauma: A review of the literature. Aust Dent J. 2000; 45:2-9.         [ Links ]

2. Ravishankar TL, Kumar MA, Ramesh N, Chaitra TR. Prevalence of traumatic dental injuries to permanent incisors among 12-year-old school children in Davangere, South India. Chin J Dent Res. 2010; 13:57-60.

3. Thelen DS, Bårdsen A. Traumatic dental injuries in an urban adolescent population in Tirana, Albania. Dent Traumatol. 2010; 26:284-90.

4. Andreasen JO, Andreasen FM, Andersson L. Textbook and color atlas of traumatic injuries to the teeth. 4th ed. Oxford: Blackwell Munksgaard; 2007.

5. Huang HM, Tsai CY, Lee HF, Lin CT, Yao WC, Chiu WT et al. Damping effects on the response of maxillary incisor subjected to a traumatic impact force: a nonlinear finite element analysis. J Dent. 2006; 34:261-8.

6. Boccaccio A, Ballini A, Pappalettere C, Tullo D, Cantore S, Desiate A. Finite Element Method (FEM), mechanobiology and biomimetic scaffolds in bone tissue engineering. Int J Biol Sci. 2011; 7:112-32.

7. Silva BR, Silva FI Jr, Moreira Neto JJS, Aguiar ASW. Finite Element Method application in dentistry: analysis of scientific production from 1999 to 2008. Int J Dent. 2009; 8:197-201.

8. Vasudeva, G. Finite element analysis: a boon to dental research. Internet J Dent Sci. 2009; 6:1-6.

9. Dejak B, Mlotkowski A. Finite element analysis of strength and adhesion of cast posts compared to glass fiber-reinforced composite resin posts in anterior teeth. J Prosthet Dent. 2011; 105:115-26.

10. Szucs A, Bujtar P, Sandor GK, Barabas J. Finite element analysis of the human mandible to assess the effect of removing an impacted third molar. J Can Dent Assoc. 2010; 76:72-7.

11. Poiate IAVP, Vasconcellos AB, Andueza A, Pola IRV, Poiate E Jr. Three dimensional finite element analyses of oral structures by computerized tomography. J Biosci Bioeng. 2008; 106:606-9.

12. Silva BR, Moreira Neto JJS, Silva FI Jr, Aguiar ASW. Finite element analysis applied to dentoalveolar trauma: methodology description. ISRN Dentistry. 2011; 16:1-7.

13. Poiate IAVP, Vasconcellos AB, Poiate E Jr, Dias KRHC. Stress distribution in the cervical region of an upper central incisor in a 3D finite element model. Braz Oral Res. 2009; 23:161-8.

14. Poiate IAVP, Vasconcellos AB, Santana RB, Poiate E Jr. Three-dimensional stress distribution in the human periodontal ligament in masticatory, parafunctional, and trauma loads: finite element analysis. J Periodontol. 2009; 80:1859-67.

15. Huang HM, Ou KL, Wang WN, Chiu WT, Lin CT, Lee SY. Dynamic finite element analysis of the human maxillary incisor under impact loading in various directions. J Endod. 2005; 31:723-7.

16. Miura J, Maeda Y. Biomechanical model of incisor avulsion: a preliminary report. Dent Traumatol. 2008; 24:454-7.

17. Stuart CH, Schwartz SA, Beeson TJ. Reinforcement of immature roots with a new resin filling material. J Endod. 2006; 32:350-3.

18. Andreasen JO, Andreasen FM, Meja`re I, Cvek M. Healing of 400 intra-alveolar root fractures. 1. Effect of pre-injury and injury factors such as sex, age, stage of root development, fracture type, location of fracture and severity of dislocation. Dent Traumatol. 2004; 20:192–202.

19. Nyashin YI, Nyashin MY. Biomechanical modelling of periodontal ligament behavior under various mechanical loads. Acta Bioeng Biomech. 2000; 2:67-74.

20. Bechtle S, Habelitz S, Klocke A, Fett T, Schneider GA. The fracture behavior of dental enamel. Biomaterials. 2010; 31:375-84.

21. Baldassiri M, Margolis HC, Beniash E. Compositional determinants of mechanical properties of enamel. J Dent Res. 2008; 87:645-9.

22. Cochrane NJ, Cai F, Huq NL, Burrow MF, Reynolds EC. New approaches to enhanced remineralization of tooth enamel. J Dent Res. 2010; 89:1187-97.

23. Poolthong S, Mori T, Swain MV. Determination of elastic modulus of dentin by small spherical diamond indenters. Dent Mater J. 2001; 20:227- 36.

24. Majorana A, Pasini S, Bardellini E, Keller E. Clinical and epidemiological study of traumatic root fractures. Dent Traumatol. 2002; 18:77-80.

25. De Las Casas EB, Cornacchia TP, Gouvêa PH, Cimini CA Jr. Abfraction and anisotropy--effects of prism orientation on stress distribution. Comput Methods Biomech Eng. 2003; 6:65-73.

26. Natali AN. Dental biomechanics. London: Taylor & Francis/CRC Press; 2003.

27. Limbert G, Middleton J, Laizans J, Dobelis M, Knets I. A transversely isotropic hyperelastic constitutive model of the PDL. Analytical and computational aspects. Comput Methods Biomech Biomed Eng. 2003; 6:337-45.

28. Natali AN, Carniel EL, Pavan PG, Sander FG, Dorow C, Geiger M. A visco-hyperelasticdamage constitutive model for the analysis of the biomechanical response of the periodontal ligament. J Biomech Eng. 2008; 130:73-9.

29. Provatidis CG. A comparative FEM-study of tooth mobility using isotropic and anisotropic models of the periodontal ligament. Finite Element Method. Med Eng Phys. 2000; 22:359-70.

30. Tanaka M, Naito T, Yokota M, Kohno M. Finite element analysis of the possible mechanism of cervical lesion formation by occlusal force. J Oral Rehabil. 2003; 30:60-7.